Geostationäre Satelliten

Beobachtungen an unseren eigenen geschaffenen Erdtrabanten, den geostationären Satelliten
ASTRA Cluster Komposit über 10h vom 20.10.12 mit 650 mm
(z. B. Astra; Kopernikus; Eutelsat etc.)
Theorie und Praxis
Vielleicht ist es schon jemanden bei einer Plutobeobachtung aufgefallen, dass während dieser auf einmal „Sterne“ durch das Okular wandern. Falls ja, dann hat der Beobachter höchst wahrscheinlich die Bekanntschaft mit einem geostationären Satelliten gemacht.
Man könnte ja einmal den Spieß herumdrehen und die Beobachtung gezielt auf einen dieser Satelliten richten. Hierbei ist z.B. der Astra Cluster schon auf sieben Einzelsatelliten angewachsen. Bei Beobachtungen von >15min sind sogar Ihre Eigenbewegungen zur Bahnstabilisierung zu sehen bzw. zu fotografieren.
Die Besonderheit bei der Beobachtung bzw. Fotografie liegt daran, dass diese ohne Nachführung des Teleskops geschieht! Hierbei nutzen wir den Vorteil, dass diese Satelliten, wie der Name schon sagt „geostationär“, mit der gleichen Zeit sich um die Erde drehen wie die Umlaufzeit der Erde ist.
Der Nachteil an dieser Sache ist aber, dass sich zwar der Satellit sich immer an der „gleichen Stelle“ über der Erde befindet, aber der Sternhimmel, welcher als Bezugspunkt zum Aufsuchen dient, sich aber „dreht“!
Um diese Problematik zu lösen, möchte ich dieses am Beispiel vom Astra Cluster demonstrieren und dann allgemein für alle geostationären Satelliten vereinfachen.
Da zur Positionsbestimmung der Satelliten uns nur sein Längengrad bekannt ist, müssen wir ab hier unsere Berechnung anfangen.
Jeder der eine Satellitenschüssel einmal aufgestellt hat findet in seiner Gebrauchsanweisung eine Angabe z.B. Astra Satellit Position = 19,2° Ost. Des weiteren findet man noch ein Diagramm o.ä. welches die Höhe über dem Horizont und den Azimut auf seinen Ort enthält.
Für uns ist nur die Angabe : 19,2° Ost interessant! Diese Angabe sagt aus, daß die „Schüssel“ auf dem Längengrad 19,2° Ost direkt im Meridian stehen muß. Oder anders gesagt in Greenwich muß man Sie 19,2° nach Osten drehen um Astra zu empfangen oder zu beobachten.
So jetzt haben wir einen Bezug zum Längengrad bzw. später zur Rektaszension aber woher bekommen wir unseren Bezug zur Höhe bzw. später zur Deklination?
Diese Information birgt der Satellit in sich selbst. Der Satellit muß direkt über dem Äquator stehen da sonst die Bahn des Satelliten nicht parallel zur Erde laufen würde. Zum Vergleich, währe der Satellit über dem Nordpol, dann währe er nach zwölf Stunden über dem Südpol und nach 24 Stunden wieder über dem Nordpol zu sehen, zum Fernsehschauen relativ uninteressant, oder?
So jetzt wissen wir, dass Astra am Äquator und bei 19,2° östlicher Länge direkt im Zenit steht. Leider sitze ich hier z.B. in Ingolstadt und dieser Ort liegt 48,75° Nord und 11,42° Ost.
Nun muß die Höhe des Satelliten in Deklination umgewandelt werden und die Länge in Rektaszension. Eine weitere Schwierigkeit besteht aber noch, die Rektaszension von Astra ändert sich mit der Zeit (Astra ist ja kein Stern!)
Ich möchte hier einen Weg zeigen die Position (Rektaszension oder dessen Stundenwinkel und Deklination) von Astra zu einer bestimmten Uhrzeit zu bestimmen.
Download als Programme : Windows Version
Um die Berechnung durchzuführen benötigen wir :
1.) Falls nur der Stundenwinkel benötigt wird:
Längengrad Beobachtungsort z.B. 48,75° Ingolstadt
Breitengrad Beobachtungsort z.B. 11,42° Ost Ingolstadt
Position des Satelliten z.B. 19,2° Ost Astra
Erdradius 6378 km
geostationärer Bahnradius 42164 km (3. Kepler Gesetz)
2.) Falls die Rektaszension erechnet werden soll:
Mitteleuropäische Zeit MEZ (Funkuhrgenauigkeit!)
Mittlere Ortssternzeit MOZ aus Jahrbuch oder PC (z.B. Ingolstadt)
An den Grafiken kann man graphisch bzw. mathematisch die Herleitung der Berechnungsformel für die Deklination, bzw. Stundenwinkel oder Rektaszension erkennen.

Stundenwinkel:
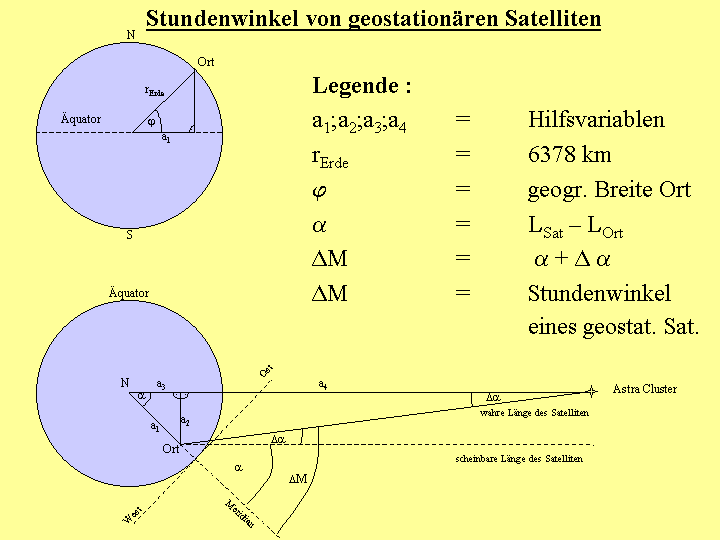

Deklination:

